La importancia del sentido numérico

Hace unos años el político británico Stephen Byers cometió un pequeño error que se hizo viral en una entrevista. Se le pidió que diera la respuesta a 7 x 8 y dio la respuesta de 54, en lugar de 56. Su error provocó el ridículo generalizado en los medios nacionales, acompañado de llamados para un mayor énfasis en memorización de ‘tablas de multiplicar’ en las escuelas. 

En septiembre pasado, el ministro de educación de Inglaterra, un hombre sin experiencia educativa, insistió en que todos los estudiantes del país deberían saberse de memoria todas las tablas de multiplicar hasta la del 12 a la edad de 9 años. 

Este requisito se ha incluido en el currículo oficial de matemáticas del Reino Unido. y me atrevo a predecir que esto llevará a niveles crecientes de ansiedad matemática y a un aumento del rechazo de los alumnos por la asignatura

Estados Unidos, sin embargo, parece estar posicionándose en el otro lado, ya que su currículo oficial (conocido como Common Core), basado en estándares concretos de aprendizaje resta énfasis a la memorización de hechos matemáticos.

Desafortunadamente, las malas interpretaciones del significado de la palabra ‘fluidez’ que aparece en el currículo nacional son comunes, y las editoriales de libros de texto continúan enfatizando la memorización, y persistiendo en tareas dañinas para el aprendizaje a largo plazo.

Los hechos matemáticos, como pueden ser las tablas de multiplicar, son importantes, pero la memorización a través de la repetición o con pruebas cronometradas es innecesaria y dañina. El error del ministro británico cuando se le pidió decir “7 x 8” provocó que la gente pidiera más trabajo de memorización en la escuela. Esto resulta algo irónico, ya que, precisamente el error que cometió fue debido a recurrir solo a la memoria y olvidarse del «sentido numérico».

Las personas que tienen sentido numérico son aquellas que pueden usar los números con flexibilidad mental. Por ejemplo, cuando se pregunta cuánto es 7 x 8, alguien con sentido numérico puede saber de memoria que es 56 pero también podría calcular que 7 x 7 es 49 y luego sumar otros 7 para llegar a 56. Otra forma sería también calcular diez veces 7 y restar dos veces 7 (70-14 = 56). De este modo, no tendrían que depender de un recuerdo lejano.

Los hechos matemáticos, en sí mismos, son una pequeña parte de las matemáticas y se aprenden mejor mediante el uso de los números en diferentes formas y situaciones. Desgraciadamente, en muchas aulas se enfocan las operaciones matemáticas de manera improductiva, dando a los estudiantes la impresión de que las operaciones matemáticas son la esencia de las matemáticas y, lo que es peor, que recordar rápidamente las operaciones matemáticas es igual a ser un buen estudiante de matemáticas. Ambas ideas son incorrectas y es fundamental que las eliminemos de las aulas, ya que contribuyen a elevar la ansiedad matemática y rechazo hacia la asignatura.  

Es útil saberse algunas operaciones matemáticas de memoria. Yo no me paro a pensar en cuánto es 8+4, porque ya me la sé. Pero aprendí hechos matemáticos usándolos en diferentes situaciones matemáticas, no practicándolos repetidamente y pasando exámenes. Crecí en la “era progresista” de Inglaterra, cuando las escuelas primarias se enfocaban en la “educación integral del niño” y no me hacían aprenderme de memoria las tablas de la suma, la resta o la multiplicación.

Esto nunca me ha llegado a suponer un perjuicio, de hecho, ahora soy profesora de matemáticas. Y eso es porque tengo sentido numérico, algo que es mucho más importante para los alumnos. Esto del sentido numérico se consigue a través de la comprensión profunda de la forma en que los números se relacionan entre sí y su reflejo en las operaciones matemáticas. 

¿Qué es el sentido numérico?

En un proyecto de investigación bastante importante, se estudió a los alumnos mientras resolvían problemas numéricos (Gray & Tall, 1994). Los estudiantes, de 7 a 13 años, habían sido agrupados por sus maestros en función de su rendimiento: bajo, medio o alto. 

Los investigadores encontraron una diferencia importante entre los estudiantes de bajo y alto rendimiento: los de alto rendimiento hacían uso del sentido numérico, los estudiantes de bajo rendimiento, no. 

Los alumnos de alto rendimiento resolvían problemas como 19 + 7 cambiando el problema a, por ejemplo, 20 + 6. Ningún alumno de bajo rendimiento llegó a utilizar el sentido numérico. 

Cuando a los estudiantes de bajo rendimiento se les dieron problemas de resta como 21-16, contaban hacia atrás comenzando en 21, lo cual es extremadamente difícil de hacer. En cambio, los estudiantes de alto rendimiento utilizaban estrategias como cambiar los números a 20 -15, que es mucho más fácil de hacer. 

Los investigadores concluyeron que los alumnos de bajo rendimiento lo son no porque sepan menos, sino porque no usan los números con flexibilidad. Esto es porque se les ha puesto en el camino equivocado, a menudo desde una edad temprana, tratando de memorizar “recetas” en lugar de interactuar con los números. de forma flexible (Boaler, 2009). 

Este camino incorrecto hace que las matemáticas se les vuelvan más difíciles de aprender y que acaben teniendo problemas de por vida con la asignatura.

El sentido numérico es la base de todas las matemáticas de alto nivel (Feikes & Schwingendorf, 2008). Cuando los estudiantes fallan en álgebra, por ejemplo, a menudo es porque no tienen sentido numérico suficiente. Para desarrollar el sentido numérico, se puede hacer uso de tareas matemáticas “ricas” (ver ejemplo a continuación).

Cuando los estudiantes se enfocan en memorizar tablas de multiplicar, a menudo memorizan hechos sin sentido numérico, lo que significa que están muy limitados en lo que pueden hacer y son propensos a cometer errores, como el que provocó el ridículo nacional del político británico. La falta de sentido numérico ha llevado a errores más catastróficos, como que el Telescopio Hubble pierda las estrellas que debía fotografiar en el espacio. El telescopio estaba buscando estrellas en cierto cúmulo pero falló debido a que alguien cometió un error aritmético en la programación del telescopio (ver noticia aquí). El sentido numérico, de importancia crítica para el desarrollo matemático de los estudiantes, se ve inhibido cuando se da más importancia a la memorización. Cuanto más enfatizamos la memorización a los estudiantes, menos dispuestos se vuelven a pensar con los números y sus relaciones y a usar y desarrollar el sentido numérico (Boaler, 2009).

El cerebro y el sentido numérico

Algunos estudiantes no son tan buenos como otros a la hora de memorizar. En un estudio reciente del cerebro (Supekar et al, 2013), se examinaron los cerebros de los estudiantes mientras se les enseñaba a memorizar datos matemáticos. Vieron que algunos estudiantes los memorizaban mucho más fácilmente que otros. Esto no será una sorpresa para el lector y muchos de nosotros probablemente asumimos que aquellos que memorizan mejor son estudiantes de mayor rendimiento o “más inteligentes”.

En Estados Unidos y Reino Unido, se les pide a los estudiantes que memoricen las tablas de multiplicar y, a veces, también las tablas de suma y resta, generalmente porque los estándares del plan de estudios recogen que los estudiantes deben ser «fluidos con los números». Pero, si atendemos a la literatura especializada, autores como Parish (Parish 2014) definen la fluidez como «saber cómo se puede componer y descomponer un número y usar esa información para ser flexible y eficiente en la resolución de problemas«. Independientemente de cuál sea nuestra opinión sobre la “fluidez”, la evidencia de la investigación apunta en una dirección: la mejor manera de desarrollar fluidez con los números es desarrollar el sentido numérico y trabajar con números de diferentes maneras, no a ciegas y memorizando sin sentido numérico.

Cuando los maestros se centran en la memorización de hechos y ponen pruebas para medir si los alumnos saben o no hechos numéricos, pueden perjudicar el aprendizaje de dos formas distintas. Veamos.

Para alrededor de un tercio de los estudiantes, el inicio de las pruebas cronometradas coincide con el comienzo de la ansiedad matemática (Boaler, 2014).

Sian Beilock y colaboradores (2011) estudiaron los cerebros de diferentes personas a través de imágenes de resonancia magnética y descubrieron que las operaciones matemáticas se almacenan en la sección de memoria de trabajo del cerebro. Pero cuando los estudiantes están estresados, como cuando hacen pruebas contrarreloj, la memoria de trabajo se bloquea y los estudiantes no pueden acceder a las operaciones matemáticas que conocen. A medida que los estudiantes se dan cuenta de que no se les dan bien las pruebas cronometradas, comienzan a desarrollar ansiedad y su confianza matemática va disminuyendo. El fenómeno del bloqueo de la memoria de trabajo y la ansiedad asociada ocurre particularmente entre el alumnado de alto rendimiento y también más en las niñas que en los niños. Las estimaciones más conservadoras sugieren que al menos un tercio de los estudiantes experimentan un estrés extremo en torno a las pruebas cronometradas. La ansiedad matemática se ha llegado a observar en alumnos de tan solo 5 años (Ramirez, et al, 2013). Así que, cuando sometemos a los estudiantes a este tipo de tareas, estamos perdiendo futuros estudiantes de matemáticas.

En los últimos años, la investigación con neuroimagen ha descubierto que los estudiantes que tienen más éxito con los problemas numéricos son aquellos que usan diferentes vías cerebrales, una que es numérica y simbólica y la otra que involucra un razonamiento más intuitivo y espacial (Park & ​​Brannon, 2013). Al final de este documento ofrecemos muchas actividades que fomentan la comprensión visual de los hechos numéricos, para permitir que se formen esas conexiones cerebrales tan importantes. 

En otro estudio, Delazer y colaboradores (2005), analizaron a dos grupos diferentes de alumnos: aquellos que utilizan el aprendizaje memorístico contra aquellos que recurren al uso de estrategias. Se observó que cada forma activa vías distintas en el cerebro y ambas son válidas para su uso diario. No obstante, el estudio encontró que aquellos que aprenden el uso de estrategias logran un rendimiento superior sobre aquellos que memorizan. Además, son capaces de resolver los problemas a la misma velocidad y muestran una mejor transferencia en nuevos problemas posteriores.

Los autores de este estudio concluyen que la automatización de hechos matemáticos debe alcanzarse a través de la comprensión de las relaciones numéricas, pensamiento y razonando sobre estrategias numéricas.

¿Por qué a las matemáticas se tratan diferente en la escuela?

Para aprender un idioma, para aprender a leer y comprender novelas o poesía, los alumnos deben saber el significado de muchas palabras. Pero ningún estudiante de inglés diría que aprender inglés consiste en memorizar y recordar rápidamente las palabras, como a menudo se hace en matemáticas. Esto se debe a que aprendemos las palabras a medida que las usamos en muchas situaciones diferentes: hablando, leyendo, escribiendo…

Por esto, los profesores de inglés no les dan a sus alumnos cientos de palabras para memorizar y luego examinarlas en pruebas contrarreloj de tiempo. Todas las asignaturas requieren la memorización de algunos hechos, pero las matemáticas son la única materia en la que los profesores creen que deben evaluarse únicamente en condiciones de tiempo. ¿Por qué tratamos las matemáticas de esta manera?

Las matemáticas suelen tener mala fama entre los alumnos, y a menudo es el área que mas disgustos genera. El uso de tareas que enfatizan la memorización de operaciones matemáticas es, en gran medida, la razón por la que los estudiantes acaban desconectándose de la asignatura. 

Muchas personas podrían argumentar que las matemáticas son diferentes a otras materias y que por ello se deben enseñar así, ya que las matemáticas buscan la obtención de respuestas correctas, y no admiten interpretación personal o manejo de significados. Este es otro concepto erróneo. El núcleo de las matemáticas es el razonamiento, es decir, pensar por qué lo que uno piensa tiene sentido y hablar sobre cuándo usar uno u otro método de cálculo (Boaler, 2013). 

Saber hechos matemáticos es solo una pequeña parte de las matemáticas y probablemente la parte menos interesante. 

Creemos que hay que dejar de ver las matemáticas como solamente cálculos. Debe haber un equilibrio entre procesos y contenidos, y los estudiantes deben aprender a calcular a través del sentido numérico, así como dedicar más tiempo a las partes menos trabajadas pero que son críticas en las matemáticas, como la resolución de problemas y razonamiento.

Cuando se enseña a los estudiantes el sentido numérico y las operaciones, es importante no mandar el mensaje de que la velocidad importa. De hecho, esto es cierto para todo en matemáticas. Existe un concepto erróneo común y perjudicial: la idea de que los estudiantes buenos en matemáticas son los estudiantes rápidos.

Trabajo con muchos matemáticos y una cosa que noto de ellos es que no son particularmente rápidos con los números, de hecho, algunos de ellos son bastante lentos.

Esto no es malo, son lentos porque piensan profunda y cuidadosamente sobre las matemáticas. Laurent Schwartz, un destacado matemático, escribió una autobiografía sobre sus días en la escuela y cómo se sentida «estúpido» porque era uno de los que pensaban más despacio de su clase (Schwartz, 2001).

Tardó muchos años en llegar a la conclusión de que ‘la rapidez no tiene una relación precisa con la inteligencia. Lo importante es comprender profundamente las cosas y sus relaciones entre sí. Aquí es donde reside la inteligencia. El hecho de ser rápido o lento no es realmente relevante.’ (Schwartz, 2001)

Lamentablemente, las clases de matemáticas “con prisas” y basadas en exámenes llevan a muchos estudiantes lentos, pero que piensan profundamente, como Schwartz, a creer que no pueden ser buenos en matemáticas.

¿Cómo desarrollar el sentido numérico?

A continuacion, recogemos algunas actividades para trabajar el sentido numérico a partir de diferentes contenidos.

Trabajando la suma y la descomposición:

• “Rómpelo” Esta actividad se puede trabajar en parejas. Un niño construye un pequeño tren con el número que quiera de policubos. A la señal de “Rómpelo”, el niño parte su tren en 2 partes y esconde una de las partes detrás de su espalda.  El otro niño tiene que pensar qué número esconde su compañero en la espalda.

• “¿Cuántos escondo?” Un alumno tiene 10 contadores y un vaso. Tiene que esconder algunos dentro del vaso y dejar otros fuera. El compañero deberá adivinar cuántos hay debajo del vaso.

• “Cierra la caja” Escribo en un papel los números del 1 al 10. Lanzando 2 dados, debemos “cerrar” el número que haya salido. Por ejemplo, lanzo los dos dados y sale 5 y 2 = 7. Puedo cerrar el 7, o puedo cerrar “6 y 1”, “5 y 2”, o “4 y 3”. El juego termina cuando logro cerrar todos los números.  Este juego permite muchas variantes y cambios de reglas. Se puede elegir tirar con uno o con dos dados a medida que avanza la partida.

Trabajando la multiplicación:

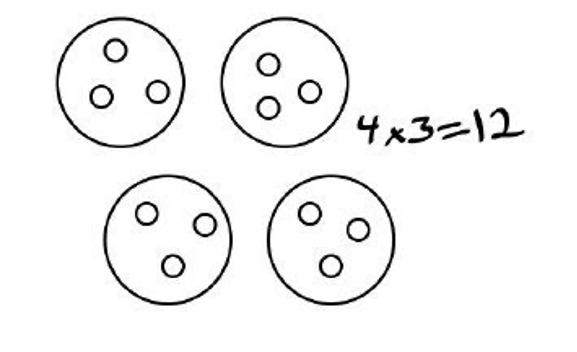
• «Pizza de pepperoni» En este juego, un niño tira un dado dos veces. La primera tirada indica el número de pizzas que tiene que dibujar. La segunda tirada indica cuántos trozos de pepperoni tiene que dibujar en cada pizza.  Después, tiene que escribir la operación matemática que conteste a la pregunta “¿Cuántas piezas de pepperoni hay en total?”

Por ejemplo: yo tiro un dado y me sale un 4, así que dibujo 4 pizzas. Después, el siguiente dado me indica un 3, así que dibujo 3 trozos de pepperoni en cada pizza. Por último, escribo 4 x 3 = 12, que me sirve para saber que tengo 12 trozos de pepperoni en total.

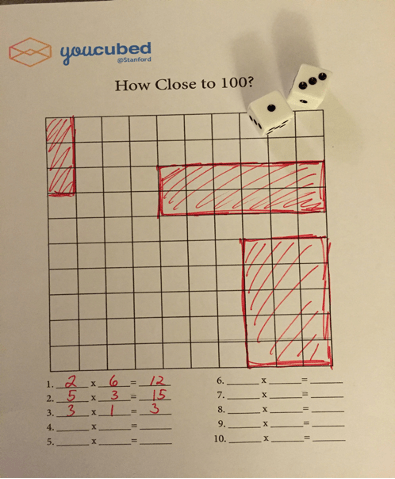
• ¿Puedes hacer 100?

Lanzando dos dados, hay que ir rellenando el tablero de 100 piezas según los que salga en los dados. El objetivo es intentar rellenar el máximo de superficie posible. ¿Puedes rellenar las 100 casillas?

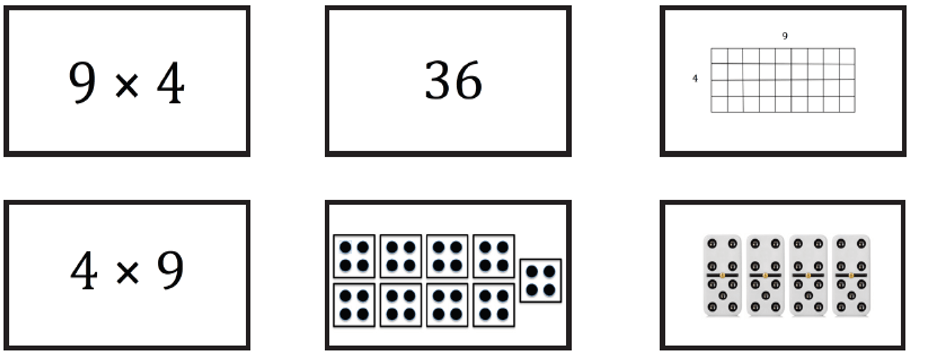
• Memory

Se pueden utilizar tarjetas con diferentes representaciones de un mismo número y jugar a emparejarlas. En la isugiente imgen se observa el número 36 con diferentes representaciones:

Artículo original:

Boaler, J., Williams, C., & Confer, A. (2015). Fluency without fear: Research evidence on the best ways to learn math facts. Reflections, 40(2), 7-12.

Artículo traducido por el autor de este blog.